Research

Aortic Shape Space Geometry

Current clinical paradigm reduces aortic geometry to a single size quantity, the maximum diameter.
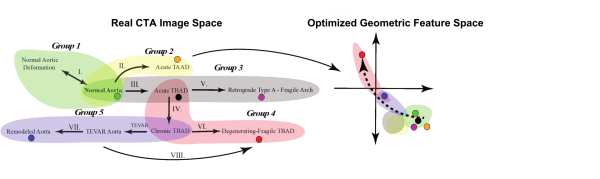
Size alone is insufficient to capture the complex shape changes in aortic disease progression.
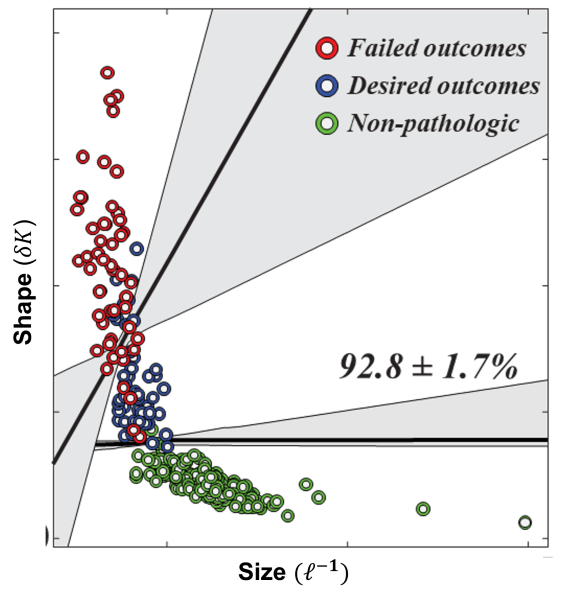
We have identified a shape parameter, fluctuations in total curvature (δK), that can distinguish between shape preserving growth in normal aortas (1-3) and rapidly fluctuating shapes that are the hallmark of disease (4-8).
Using a cohort of patients without aortic pathology, a cohort of TEVAR patients, and machine learning methods, δK was able to distinguish patients without aortic pathology, patients with TEVAR who had positive outcomes, and patients with TEVAR who had failed outcomes with over 92% accuracy.

We map the aortic surface to a unit sphere to obtain independent measures of shape using surface normals (N_i ).
Gradients in N_i give the per-vertex principal curvatures and the per-vertex shape operator (S_i ) is calculated using the Rusinkiewicz algorithm [IEEE 3DPVT 2004].
To minimize noise, the aorta is partitioned to calculate the local integrated Gaussian curvature defined as the product of the partition’s area and mean Gaussian curvature, K_j=A_j κ ̅gj.
K_j is equivalent to the signed partition area, A ̃j, mapped out by the normals projected onto the unit sphere.

K_j and A ̃j are topologic invariants. We define aortic shape by studying the statistics of the first and second distribution moments of K_j,⟨K⟩ and δK, respectively.

Seal Zone Stability in Endovascular Repairs

In traditional invasive open aortic surgery, a polymer tube graft is sutured to the aorta.
In EVAR and TEVAR, the endograft and aorta are held together simply by adhesive forces over a short region of the repair called the seal zone.
Seal zone failure can lead to endoleaks where blood flows in between the endograft and aorta.
Endoleaks lead to repeat re-pressurization of the weakened aortic wall and increases the risk of aortic rupture and patient death.

Our hypothesis: geometric incompatibility dictates interfacial stability

There is a competition between destabilizing displacement forces and loads acting on the endograft and stabilizing fixation forces.
We apply fracture mechanics with a cohesive zone model for FEM to describe seal zone failure.
Loss of seal correlates with the appearance of high stress in the aortic neck.
The elasto-adhesive seal model balances the available elastic energy in the aortic neck with the interfacial energy.

Stress Focusing Induced by Surgical Procedures

Surgical anatomy creates non-native geometries. This causes mechano-geometric compatibility problems and leads to physical stresses in the surrounding tissue.

How is anastomotic geometry linked to healing?

Leakage and bacterial infection are dreaded complications from gastrointestinal anastomoses.

Global failure of fistula maturation, poor vein dilation, or focal venous stenosis often occur in arteriovenous fistula anastomoses in hemodialysis patients.

We believe that anastomotic shape, as dictated by surgical construction and tissue anatomy, influences the tissue’s distribution of and response to mechanical stress.

Remodeling of collagen fibers

Using animal models of bowel and arteriovenous fistula anastomoses, micro-computed tomography, and finite element simulations, we want to fully capture the dynamic interplay between local tissue remodeling and morphoelasticity.

We have developed models of collagen remodeling by fiber re-orientation along directions of principal stress.

Normal fiber distributions in tissues show one fiber family in (A) longitudinal and (B) circular muscle layers but two fiber families in the (C) submucosal layer.

Interfacial Adhesion, Behavior, and Surface Topology

To stick or not to stick?

Complex natural interfaces have non-linear geometries and their biological functions depend on their mechanical properties.

The evolution of wrinkles and folds in arteries is sensitive to the collagen fiber reinforced structure of the arterial wall.

Actuation of a surface from smooth to wrinkled induces topography-driven surface renewal that prevents foulant build-up.

Generalized collapse phase diagram of lipid monolayers

Lipid monolayers at an air/water interface, for example lung surfactant, exhibit rich surface morphology and behavior upon compression that is tunable with temperature and composition. Monolayer collapse is an elastic instability where the film undergoes in-plane or out-of-plane displacement.